너비우선 탐색이라고도 불리는 BFS 알고리즘은 그래프 탐색 알고리즘중 하나이다. BFS 알고리즘은 한 갈림길에서 연결되는 모든 모든 길을 다 탐색하기 때문에 가중치가 없는 그래프에서 최단거리를 찾는데 활영 할 수 있다. 특히 타 알고리즘과 달리 무한한 길이의 경로에서도 탐색을 진행 할 수 있다는 차이가 있다. 이러한 특성은 순환마디가 존재 할 수 있는 큐브의 해법 탐색에서 유용하게 사용 될 수 있다. 다익스트라나 DFS는 큐브의 순환마디에 걸릴 수 있지만 BFS는 큐브의 어떤 상황에서도 최단 해법을 찾을 수 있음을 보장한다. 따라서 나는 BFS 알고리즘을 활용하여 큐브의 최단 해법을 탐색하는, 특히 시간복잡도 상에서 문제가 말생하지 않는 2×2 큐브에 대한 프로그램을 제작하였다.
우선 3차원 형태의 큐브를 어떻게 입력을 받고 저장 할 것인지에 대해 고민해볼 필요가 있었다. 3차원 배열, 큐브의 모서리 형태 저장과 같은 다양한 방식이 있었지만 구현이 간단하고, 큰 메모리를 차지하지 않는 전개도 방식으로 저장하기로 하였다.
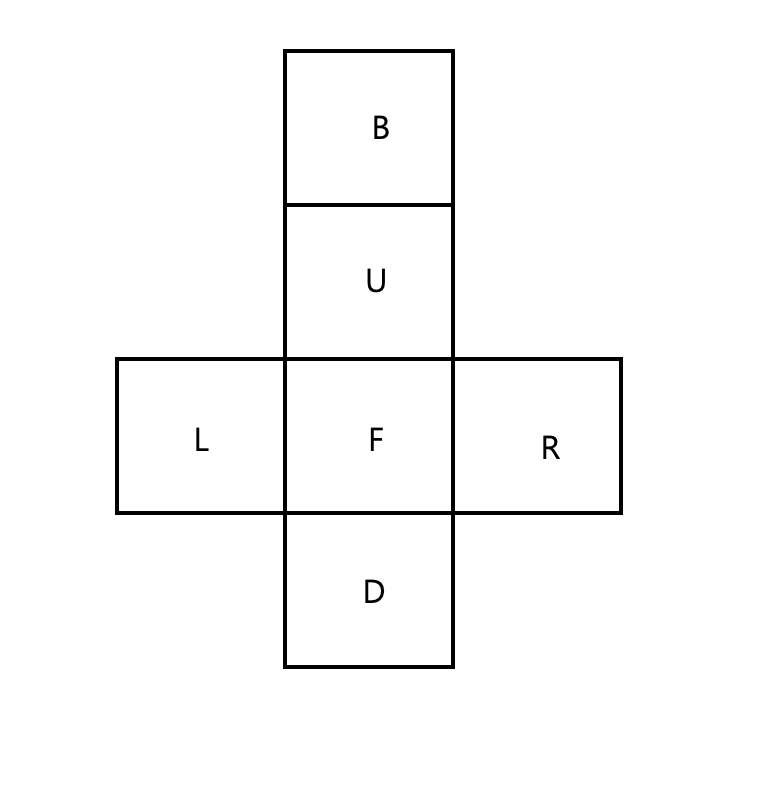
3차원의 배열을 선언하고 관리하기에는 어려움이 있으므로 cube 를 저장하는 구조체를 하나 정의하였다.
struct cube{
char F[2][2];
char B[2][2];
char U[2][2];
char D[2][2];
char L[2][2];
char R[2][2];
};이제 큐브를 회전시키는 함수를 만들어야 한다. 2×2 큐브에서 가능한 회전은 R, L, U, D, F, B 그리고 각 회전에 대한 반시계 방향 회전(프라임) 회전이 있어 총 12개의 회전이 있다. 이 부분에서 제일 많은 시간을 투자했고 구현하는데 가장 많은 어려움이 있었다. 구현한 소스코드는 아래와 같다.
cube Rotate_R(cube cu){
cube re = cu;
re.U[0][1] = cu.F[0][1];
re.U[1][1] = cu.F[1][1];
re.B[0][1] = cu.U[0][1];
re.B[1][1] = cu.U[1][1];
re.D[0][1] = cu.B[0][1];
re.D[1][1] = cu.B[1][1];
re.F[0][1] = cu.D[0][1];
re.F[1][1] = cu.D[1][1];
re.R[0][0] = cu.R[1][0];
re.R[0][1] = cu.R[0][0];
re.R[1][0] = cu.R[1][1];
re.R[1][1] = cu.R[0][1];
return re;
}
cube Rotate_L(cube cu) {
cube re = cu;
re.U[0][0] = cu.B[0][0];
re.U[1][0] = cu.B[1][0];
re.B[0][0] = cu.D[0][0];
re.B[1][0] = cu.D[1][0];
re.D[0][0] = cu.F[0][0];
re.D[1][0] = cu.F[1][0];
re.F[0][0] = cu.U[0][0];
re.F[1][0] = cu.U[1][0];
re.L[0][0] = cu.L[1][0];
re.L[0][1] = cu.L[0][0];
re.L[1][0] = cu.L[1][1];
re.L[1][1] = cu.L[0][1];
return re;
}
cube Rotate_U(cube cu) {
cube re = cu;
re.B[1][0] = cu.L[0][1];
re.B[1][1] = cu.L[0][0];
re.R[0][0] = cu.B[1][1];
re.R[0][1] = cu.B[1][0];
re.F[0][0] = cu.R[0][0];
re.F[0][1] = cu.R[0][1];
re.L[0][0] = cu.F[0][0];
re.L[0][1] = cu.F[0][1];
re.U[0][0] = cu.U[1][0];
re.U[0][1] = cu.U[0][0];
re.U[1][0] = cu.U[1][1];
re.U[1][1] = cu.U[0][1];
return re;
}
cube Rotate_D(cube cu) {
cube re = cu;
re.F[1][0] = cu.R[1][0];
re.F[1][1] = cu.R[1][1];
re.R[1][0] = cu.B[0][1];
re.R[1][1] = cu.B[0][0];
re.B[0][1] = cu.L[1][0];
re.B[0][0] = cu.L[1][1];
re.L[1][0] = cu.F[1][0];
re.L[1][1] = cu.F[1][1];
re.D[0][0] = cu.D[1][0];
re.D[0][1] = cu.D[0][0];
re.D[1][0] = cu.D[1][1];
re.D[1][1] = cu.D[0][1];
return re;
}
cube Rotate_F(cube cu) {
cube re = cu;
re.U[1][0] = cu.L[1][1];
re.U[1][1] = cu.L[0][1];
re.L[0][1] = cu.D[0][0];
re.L[1][1] = cu.D[0][1];
re.D[0][0] = cu.R[0][0];
re.D[0][1] = cu.R[1][0];
re.R[0][0] = cu.U[1][0];
re.R[1][0] = cu.U[1][1];
re.F[0][0] = cu.F[1][0];
re.F[0][1] = cu.F[0][0];
re.F[1][0] = cu.F[1][1];
re.F[1][1] = cu.F[0][1];
return re;
}
cube Rotate_B(cube cu) {
cube re = cu;
re.U[0][0] = cu.R[0][1];
re.U[0][1] = cu.R[1][1];
re.R[0][1] = cu.D[1][1];
re.R[1][1] = cu.D[1][0];
re.D[1][0] = cu.L[0][0];
re.D[1][1] = cu.L[1][0];
re.L[0][0] = cu.U[0][0];
re.L[1][0] = cu.U[0][1];
re.B[0][0] = cu.B[1][0];
re.B[0][1] = cu.B[0][0];
re.B[1][0] = cu.B[1][1];
re.B[1][1] = cu.B[0][1];
return re;
}
cube Rotate_R_Prime(cube cu){
return Rotate_R(Rotate_R(Rotate_R(cu)));
}
cube Rotate_L_Prime(cube cu){
return Rotate_L(Rotate_L(Rotate_L(cu)));
}
cube Rotate_U_Prime(cube cu){
return Rotate_U(Rotate_U(Rotate_U(cu)));
}
cube Rotate_D_Prime(cube cu){
return Rotate_D(Rotate_D(Rotate_D(cu)));
}
cube Rotate_F_Prime(cube cu){
return Rotate_F(Rotate_F(Rotate_F(cu)));
}
cube Rotate_B_Prime(cube cu){
return Rotate_B(Rotate_B(Rotate_B(cu)));
}우선 시계 방향 회전에 대해서는 일일이 구현을 해 주었다. 그리고 반시계방향(프라임) 회전은 시계방향 회전을 세번 진행하는것으로 간단히 만들었다. 왜 프라임을 따로 만들었는지 궁금 할 수도 있겠지다. 만약 프라임이 없으면 한번에 할 수 있는 회전을 세번 하므로 최단 횟수와 방법이 정확히 출력 될 수 있다.
이제 제일 중요한 BFS 탐색이다. 탐색을 진행할 큐브의 상태를 저장하는 bfs 큐와 해당 상태까지 오는데 사용한 회전을 저장한 way 큐를 따로 생성하였다. BFS탐색은 탐색할 상태에서 모든 가능한 회전을 다시 큐에 집어넣는 방식으로 진행하였다. 만약에 현재 상태가 큐브가 다 맞춰진 상태라면 최단 해법과 회전의 수를 출력하고 반복문을 탈출해 종료하도록 하였다.
vector<char> tm;
bfs.push(input);
way.push(tm);
while(!bfs.empty()){
vector<char> tmp = way.front();
cube cu = bfs.front();
bfs.pop();
way.pop();
if(isCorrect(cu)){
printf("Find!\n ");
printf("%d rotates\n", tmp.size());
for(int i=0;i<tmp.size(); i++){
printf("%c ", tmp[i]);
}
break;
}
else{
vector<char> tmp_R = tmp;
tmp_R.push_back('R');
bfs.push(Rotate_R(cu));
way.push(tmp_R);
vector<char> tmp_R_P = tmp;
tmp_R_P.push_back('r');
bfs.push(Rotate_R_Prime(cu));
way.push(tmp_R_P);
vector<char> tmp_L = tmp;
tmp_L.push_back('L');
bfs.push(Rotate_L(cu));
way.push(tmp_L);
vector<char> tmp_L_P = tmp;
tmp_L_P.push_back('l');
bfs.push(Rotate_L_Prime(cu));
way.push(tmp_L_P);
vector<char> tmp_U = tmp;
tmp_U.push_back('U');
bfs.push(Rotate_U(cu));
way.push(tmp_U);
vector<char> tmp_U_P = tmp;
tmp_U_P.push_back('u');
bfs.push(Rotate_U_Prime(cu));
way.push(tmp_U_P);
vector<char> tmp_D = tmp;
tmp_D.push_back('D');
bfs.push(Rotate_D(cu));
way.push(tmp_D);
vector<char> tmp_D_P = tmp;
tmp_D_P.push_back('d');
bfs.push(Rotate_D_Prime(cu));
way.push(tmp_D_P);
vector<char> tmp_F = tmp;
tmp_F.push_back('F');
bfs.push(Rotate_F(cu));
way.push(tmp_F);
vector<char> tmp_F_P = tmp;
tmp_F_P.push_back('f');
bfs.push(Rotate_F_Prime(cu));
way.push(tmp_F_P);
vector<char> tmp_B = tmp;
tmp_B.push_back('B');
bfs.push(Rotate_B(cu));
way.push(tmp_B);
vector<char> tmp_B_P = tmp;
tmp_B_P.push_back('b');
bfs.push(Rotate_B_Prime(cu));
way.push(tmp_B_P);
}
}아래는 최종적으로 작성한 소스코드로 입력을 받고, 큐브가 다 맞춰진 상태인지를 확인하는 함수가 추가되었다.
#include <stdio.h>
#include <algorithm>
#include <queue>
using namespace std;
const char face[6] = {'F', 'B', 'U', 'D', 'L', 'R'};
struct cube{
char F[2][2];
char B[2][2];
char U[2][2];
char D[2][2];
char L[2][2];
char R[2][2];
};
queue<cube> bfs;
queue<vector<char> > way;
cube input;
void Inputer(int n, int i, int j, char tmp){
if(n==0){
input.F[i][j] = tmp;
return ;
}
if(n==1){
input.B[i][j] = tmp;
return ;
}
if(n==2){
input.U[i][j] = tmp;
return ;
}
if(n==3){
input.D[i][j] = tmp;
return ;
}
if(n==4){
input.L[i][j] = tmp;
return ;
}
if(n==5){
input.R[i][j] = tmp;
return ;
}
}
cube Rotate_R(cube cu){
cube re = cu;
re.U[0][1] = cu.F[0][1];
re.U[1][1] = cu.F[1][1];
re.B[0][1] = cu.U[0][1];
re.B[1][1] = cu.U[1][1];
re.D[0][1] = cu.B[0][1];
re.D[1][1] = cu.B[1][1];
re.F[0][1] = cu.D[0][1];
re.F[1][1] = cu.D[1][1];
re.R[0][0] = cu.R[1][0];
re.R[0][1] = cu.R[0][0];
re.R[1][0] = cu.R[1][1];
re.R[1][1] = cu.R[0][1];
return re;
}
cube Rotate_L(cube cu) {
cube re = cu;
re.U[0][0] = cu.B[0][0];
re.U[1][0] = cu.B[1][0];
re.B[0][0] = cu.D[0][0];
re.B[1][0] = cu.D[1][0];
re.D[0][0] = cu.F[0][0];
re.D[1][0] = cu.F[1][0];
re.F[0][0] = cu.U[0][0];
re.F[1][0] = cu.U[1][0];
re.L[0][0] = cu.L[1][0];
re.L[0][1] = cu.L[0][0];
re.L[1][0] = cu.L[1][1];
re.L[1][1] = cu.L[0][1];
return re;
}
cube Rotate_U(cube cu) {
cube re = cu;
re.B[1][0] = cu.L[0][1];
re.B[1][1] = cu.L[0][0];
re.R[0][0] = cu.B[1][1];
re.R[0][1] = cu.B[1][0];
re.F[0][0] = cu.R[0][0];
re.F[0][1] = cu.R[0][1];
re.L[0][0] = cu.F[0][0];
re.L[0][1] = cu.F[0][1];
re.U[0][0] = cu.U[1][0];
re.U[0][1] = cu.U[0][0];
re.U[1][0] = cu.U[1][1];
re.U[1][1] = cu.U[0][1];
return re;
}
cube Rotate_D(cube cu) {
cube re = cu;
re.F[1][0] = cu.R[1][0];
re.F[1][1] = cu.R[1][1];
re.R[1][0] = cu.B[0][1];
re.R[1][1] = cu.B[0][0];
re.B[0][1] = cu.L[1][0];
re.B[0][0] = cu.L[1][1];
re.L[1][0] = cu.F[1][0];
re.L[1][1] = cu.F[1][1];
re.D[0][0] = cu.D[1][0];
re.D[0][1] = cu.D[0][0];
re.D[1][0] = cu.D[1][1];
re.D[1][1] = cu.D[0][1];
return re;
}
cube Rotate_F(cube cu) {
cube re = cu;
re.U[1][0] = cu.L[1][1];
re.U[1][1] = cu.L[0][1];
re.L[0][1] = cu.D[0][0];
re.L[1][1] = cu.D[0][1];
re.D[0][0] = cu.R[0][0];
re.D[0][1] = cu.R[1][0];
re.R[0][0] = cu.U[1][0];
re.R[1][0] = cu.U[1][1];
re.F[0][0] = cu.F[1][0];
re.F[0][1] = cu.F[0][0];
re.F[1][0] = cu.F[1][1];
re.F[1][1] = cu.F[0][1];
return re;
}
cube Rotate_B(cube cu) {
cube re = cu;
re.U[0][0] = cu.R[0][1];
re.U[0][1] = cu.R[1][1];
re.R[0][1] = cu.D[1][1];
re.R[1][1] = cu.D[1][0];
re.D[1][0] = cu.L[0][0];
re.D[1][1] = cu.L[1][0];
re.L[0][0] = cu.U[0][0];
re.L[1][0] = cu.U[0][1];
re.B[0][0] = cu.B[1][0];
re.B[0][1] = cu.B[0][0];
re.B[1][0] = cu.B[1][1];
re.B[1][1] = cu.B[0][1];
return re;
}
cube Rotate_R_Prime(cube cu){
return Rotate_R(Rotate_R(Rotate_R(cu)));
}
cube Rotate_L_Prime(cube cu){
return Rotate_L(Rotate_L(Rotate_L(cu)));
}
cube Rotate_U_Prime(cube cu){
return Rotate_U(Rotate_U(Rotate_U(cu)));
}
cube Rotate_D_Prime(cube cu){
return Rotate_D(Rotate_D(Rotate_D(cu)));
}
cube Rotate_F_Prime(cube cu){
return Rotate_F(Rotate_F(Rotate_F(cu)));
}
cube Rotate_B_Prime(cube cu){
return Rotate_B(Rotate_B(Rotate_B(cu)));
}
bool isCorrect(cube cu){
if(cu.F[0][0] != cu.F[0][1] || cu.F[0][1] != cu.F[1][0] || cu.F[1][0] != cu.F[1][1]){
return false;
}
if(cu.B[0][0] != cu.B[0][1] || cu.B[0][1] != cu.B[1][0] || cu.B[1][0] != cu.B[1][1]){
return false;
}
if(cu.U[0][0] != cu.U[0][1] || cu.U[0][1] != cu.U[1][0] || cu.U[1][0] != cu.U[1][1]){
return false;
}
if(cu.D[0][0] != cu.D[0][1] || cu.D[0][1] != cu.D[1][0] || cu.D[1][0] != cu.D[1][1]){
return false;
}
if(cu.L[0][0] != cu.L[0][1] || cu.L[0][1] != cu.L[1][0] || cu.L[1][0] != cu.L[1][1]){
return false;
}
if(cu.R[0][0] != cu.R[0][1] || cu.R[0][1] != cu.R[1][0] || cu.R[1][0] != cu.R[1][1]){
return false;
}
return true;
}
int main(){
//전개도 형태로 입력
/*
B
U
L F R
D
*/
for(int n=0;n<6;n++){
printf("%c\n", face[n]);
for(int i=0;i<2;i++){
for(int j=0;j<2;j++){
char tmp;
scanf(" %c", &tmp);
//printf("%c", tmp);
Inputer(n, i, j, tmp);
}
}
}
vector<char> tm;
bfs.push(input);
way.push(tm);
while(!bfs.empty()){
vector<char> tmp = way.front();
cube cu = bfs.front();
bfs.pop();
way.pop();
if(isCorrect(cu)){
printf("Find!\n ");
printf("%d rotates\n", tmp.size());
for(int i=0;i<tmp.size(); i++){
printf("%c ", tmp[i]);
}
break;
}
else{
vector<char> tmp_R = tmp;
tmp_R.push_back('R');
bfs.push(Rotate_R(cu));
way.push(tmp_R);
vector<char> tmp_R_P = tmp;
tmp_R_P.push_back('r');
bfs.push(Rotate_R_Prime(cu));
way.push(tmp_R_P);
vector<char> tmp_L = tmp;
tmp_L.push_back('L');
bfs.push(Rotate_L(cu));
way.push(tmp_L);
vector<char> tmp_L_P = tmp;
tmp_L_P.push_back('l');
bfs.push(Rotate_L_Prime(cu));
way.push(tmp_L_P);
vector<char> tmp_U = tmp;
tmp_U.push_back('U');
bfs.push(Rotate_U(cu));
way.push(tmp_U);
vector<char> tmp_U_P = tmp;
tmp_U_P.push_back('u');
bfs.push(Rotate_U_Prime(cu));
way.push(tmp_U_P);
vector<char> tmp_D = tmp;
tmp_D.push_back('D');
bfs.push(Rotate_D(cu));
way.push(tmp_D);
vector<char> tmp_D_P = tmp;
tmp_D_P.push_back('d');
bfs.push(Rotate_D_Prime(cu));
way.push(tmp_D_P);
vector<char> tmp_F = tmp;
tmp_F.push_back('F');
bfs.push(Rotate_F(cu));
way.push(tmp_F);
vector<char> tmp_F_P = tmp;
tmp_F_P.push_back('f');
bfs.push(Rotate_F_Prime(cu));
way.push(tmp_F_P);
vector<char> tmp_B = tmp;
tmp_B.push_back('B');
bfs.push(Rotate_B(cu));
way.push(tmp_B);
vector<char> tmp_B_P = tmp;
tmp_B_P.push_back('b');
bfs.push(Rotate_B_Prime(cu));
way.push(tmp_B_P);
}
}
return 0;
}코드가 완성된 후 테스트를 진행해 보았다. 다양한 경우에 대해 모두 정상적으로 작동됨을 확인 할 수 있었다.
이번 탐구는 알고리즘 적으로는 어려운 내용은 크게 없었지만 구현이 복잡하고 어려웠다. 특히 큐브의 회전을 구현하는 과정에서 계속 실수가 발생하기도 하였다. 아마도 코너를 기록하는 방식으로 큐브를 저장했으면 회전의 구현이 더 쉬었을 것 같다.
이 프로그램을 활용해 추후 2×2 큐브의 최단 해법 공식에 대해 탐구 해 보고 싶다. 일정한 규칙을 찾거나, 아니면 이것이 불가능함을 증명해 보고자 한다.